Fonctions numériques
1 Propriétés des fonctions
1.1 Ensemble de définition
Soit f une fonction de E dans F.
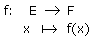
NB: Certains éléments de F peuvent ne pas avoir d'antécédent par f. Par contre, tous les éléments de E ont une image unique par f.
Deux cas se présentent:
- soit E est donné,
- soit il faut le déterminer.
COMMENT DETERMINER L'ENSEMBLE DE DEFINITION D'UNE FONCTION ?
Il faut retenir:
- lorsque f est une fonction rationnelle, le dénominateur doit toujours être différent de 0.
- toute fonction polynôme est définie sur entier.
- une expression sous radical doit toujours être positive ou nulle.
ATTENTION !!!! Les fonctions étudiées sont toujours définies sur des intervalles ou des réunions d'intervalles.
1.2 Egalité de deux fonctions
Deux fonctions f et g sont égales si et seulement si:
- elles ont le même ensemble de définition:
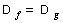
- pour tout x de cet ensemble de définition, f(x)=g(x).
Il ne faut jamais oublier la première condition, qui est nécessaire.

1.3 Bijection
METHODE :
Pour déterminer si une application f de E dans F est une bijection, on peut résoudre l'équation f(x)=b où b est un élément quelconque de F.
L'application f est bijective si et seulement si pour tout b de F, l'équation f(x)=b admet une solution et une seule dans E.
2 Elements de symetrie d'une courbe
Cela permet de réduire l'étude d'une fonction sur un intervalle réduit de l'ensemble de définition de cette fonction.
Mais, attention, il faut toujours expliquer pourquoi, à partir de la connaissance de f sur un petit intervalle, on peut connaître f sur son ensemble de définition entier.
2.1 Parité
Rappels:
Les fonctions 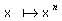
Les fonctions 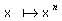 sont paires quand n est un entier pair et impaires quand n est un entier impair.
sont paires quand n est un entier pair et impaires quand n est un entier impair.
Dans un repère orthonormal :
- la courbe représentative d'une fonction paire est symétrique par rapport à l'axe (Oy).
- la courbe représentative d'une fonction impaire est symétrique par rapport à l'origine O.
Exemples : Les paraboles 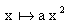
L'axe de symétrie (O y) est appelé l'axe de la parabole.
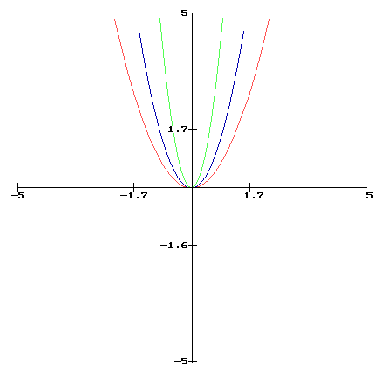
Les hyperboles 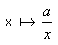
L'origine O du repère est le centre de l'hyperbole.
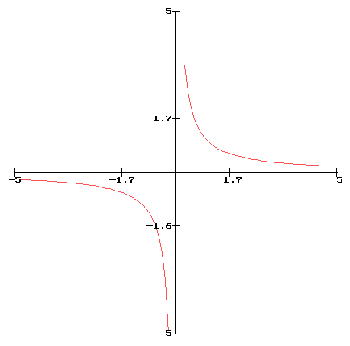
METHODES
Pour déterminer si une fonction est paire ou impaire:
- Il faut commencer par vérifier que D est symétrique par rapport à O.
- Lors de l'étude d'une fonction f, on ne parle de parité que si f est réellement paire ou impaire, sinon on ne dit rien.
- Pour montrer que f est paire ou impaire, il faut toujours faire deux vérifications: la symétrie de D par rapport à O puis on compare f(x) avec f(-x).
2.2 Eléments de symétrie
AXE DE SYMÉTRIE x=a avec a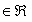
Pour montrer qu'une fonction admet la droite d'équation x=a comme axe de symétrie, il existe 3 méthodes:
- On vérifie que pour tout x de, (2a-x), puis que f(2a-x)=f(x).
- On vérifie que pour tout h de, (a-h) et (a+h)
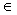 , puis que f(a-h)=f(a+h).
, puis que f(a-h)=f(a+h). - On utilise le changement de repère: il s'agit de montrer que
(
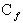 )
est la courbe représentative
d'une fonction F paire dans le repère
(
)
est la courbe représentative
d'une fonction F paire dans le repère
(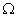 , i, j ),
, i, j ),
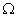 ayant pour coordonnées (a; 0) dans le repère
(O, i, j ). F vérifie alors Y=F(X). On obtient les formules suivantes de changement de repère :
ayant pour coordonnées (a; 0) dans le repère
(O, i, j ). F vérifie alors Y=F(X). On obtient les formules suivantes de changement de repère :
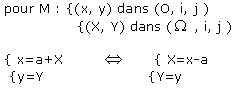
Et enfin, on vérifie que F(-X)=F(X): donc F est paire et la courbe représentative de F est symétrique par rapport à (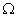 , j).
, j).
CENTRE DE SYMÉTRIE A(a, b) avec a et b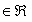
Pour montrer qu'une fonction admet le point A comme centre de symétrie, il existe 3 méthodes:
- On vérifie que pour tout x de, (2a-x), puis que f(2a-x)+f(x)=2b.
- On vérifie que pour tout h de, (a-h) et (a+h), puis que f(a-h)+f(a+h)=2b.
- On utilise le changement de repère: il s'agit de montrer que
(
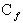 ) est la courbe représentative
d'une fonction F impaire dans le repère
(
) est la courbe représentative
d'une fonction F impaire dans le repère
(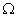 , i, j ),
, i, j ),
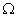 ayant pour coordonnées (a;b) dans le repère (O, i, j ). F vérifie alors Y=F(X).
ayant pour coordonnées (a;b) dans le repère (O, i, j ). F vérifie alors Y=F(X).
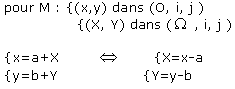
On obtient les formules suivantes de changement de repère :
Et enfin, on vérifie que F(-X)= -F(X): donc F est impaire et, origine du nouveau repère, est centre de symétrie de la courbe représentative de F.
3 Sens de variation : opération et composition
Voici un tableau à connaître par cœur :
| f | g | Opération : * | Variations f*g |
| Croissante | K*f | Décroissante si k<0 Croissante si k>0 |
|
| Décroissante | K*f | Décroissante si k>0 Croissante si k<0 |
|
| Croissante | Croissante | f + g | Croissante |
| Décroissante | Décroissante | f + g | Décroissante |
| Croissante | Croissante | f.g avec f >=0 et g >= 0 | Croissante |
| Décroissante | Décroissante | f.g avec f>=0 et g>=0 | Décroissante |
| Croissante sur E | Croissante sur E' avec E' 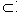 E E |
gof | Croissante |
| Croissante sur E | Décroissante sur E' avec E' 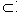 E E |
gof | Décroissante |
| Décroissante sur E | Croissante sur E' avec E' 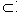 E E |
gof | Décroissante |
| Décroissante sur E | Décroissante sur E' avec E'  E E |
gof | Croissante |
Remarque sur les compositions de fonction
- pour obtenir l'expression de gof, il faut exprimer en premier g(x) en fonction de x, puis remplacer x par l'expression de f(x).
- en général, gof est différent de fog, d'où la nécessité de faire attention à l'ordre des calculs.
Quelques remarques sur les fonctions majorées
- si un majorant M est donné par l'énoncé, étudier directement le signe de M-f(x).
- Attention, il ne faut pas confondre un maximum et un majorant.
- le tableau de variation donne souvent des informations importantes.
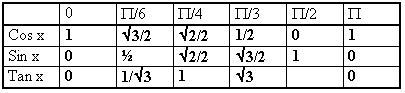
4 Fonctions circulaires
Rappel :
- La fonction sinus est définie sur R, elle est impaire et périodique de période 2p.
- La fonction cosinus est définie sur R, elle est paire et périodique de période 2p.
Ainsi, grâce à la périodicité et la parité des fonctions trigonométriques, on peut restreindre l'étude de ces fonctions à un intervalle réduit.
ASTUCE :
- Il faut apprendre par cœur les formules de trigonométrie.
- Il faut utiliser le cercle trigonométrique le plus souvent possible afin de vérifier les résultats ou tout simplement retrouver des formules.
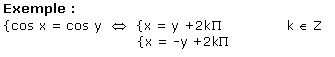
- Si f a pour période T, on étudie f sur [a, a+T]
- Si f est impaire ou paire, on étudie f sur [-T/2, T/2]