Angles orientés
1 Angles orientés
1.1 Définitions
Dans les angles orientés, il y a nécessité (comme le nom l'indique) d'orienter le cercle; c'est-à-dire qu'on définit sur le cercle C(O;R) un sens direct, positif et le sens contraire dit indirect ou négatif. Ainsi on dit souvent que sur un cercle, le sens inverse des aiguilles d'une montre est le sens trigonométrique.
DEFINITION : Un cercle trigonométrique est un cercle orienté de rayon 1.
Le plan est dit orienté quand tous les cercles du plan sont orientés positivement. (c'est à dire dans le même sens que le sens initial.)
DEFINITION : si on a deux vecteurs 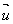 et
et 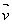 , l'angle formé par
, l'angle formé par 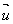 et
et 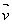 se note
se note 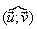 .
.
On note  une mesure
quelconque de l'angle orienté
une mesure
quelconque de l'angle orienté 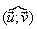 ;
il y a une infinité de mesures de cet angles ;si
a et b sont deux mesures de
;
il y a une infinité de mesures de cet angles ;si
a et b sont deux mesures de
 on peut
cependant établir le lien suivant a = b (2p)
on peut
cependant établir le lien suivant a = b (2p)
Cela signifie qu'il existe k entier naturel tel que b = a +2k.p
ATTENTION: on lit (2 p ) "modulo 2 p " et il faut faire attention à toujours le mettre lors des égalités d'angle car on peut avoir des modulos, 2p, etc…
Ainsi il y a plusieurs mesures de  mais on va en choisir une par convention : on choisit pour cela un
intervalle de référence ]-p ; p]; et l'angle
mais on va en choisir une par convention : on choisit pour cela un
intervalle de référence ]-p ; p]; et l'angle
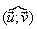 admet une seule mesure dans cet intervalle appelée mesure
principale.Dans la pratique on retranche ou on ajoute toujours 2p, k fois, pour
tomber dans l'intervalle
]-p ; p].
admet une seule mesure dans cet intervalle appelée mesure
principale.Dans la pratique on retranche ou on ajoute toujours 2p, k fois, pour
tomber dans l'intervalle
]-p ; p].
1.2 Remarques
Remarque : un angle droit est un angle où  = p/2 (p)
et non pas (2p). En effet si
= p/2 (p)
et non pas (2p). En effet si  = p/2 (2p), on dit que
(u;v) est un angle droit dans le sens positif. Mais si
= p/2 (2p), on dit que
(u;v) est un angle droit dans le sens positif. Mais si  = -p/2 (2p), alors l'angle (u;v) est un angle
droit dans le sens indirect.
= -p/2 (2p), alors l'angle (u;v) est un angle
droit dans le sens indirect.
Remarque: si 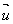 et
et 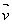 sont colinéaires :
sont colinéaires :
- de même sens alors
 =0 (2p)= 2kp
=0 (2p)= 2kp - de sens contraires alors
 =p(2p) = (2k+1).
=p(2p) = (2k+1).
Ce sont les mesures principales car on peut aussi dire dans le dernier cas que
 =-p
ou
=-p
ou  =3p, etc….
=3p, etc….
On peut dire aussi que  =0(p) et
ça signifie que
=0(p) et
ça signifie que 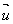 et
et
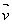 sont colinéaires, de même sens ou non.
sont colinéaires, de même sens ou non.
On peut donc utiliser les angles orientés pour montrer que 2 vecteurs sont colinéaires :finalement cela montre qu' on a des équivalences:
 = 0(2p)
<->
= 0(2p)
<-> 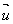 et
et 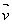 colinéaires
de même sens
colinéaires
de même sens =
p(2p) <->
=
p(2p) <->
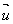 et
et
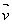 colinéaires de sens contraires.
colinéaires de sens contraires.
1.3 Propriétés
Propriétés:
- (u;v)= - (v;u) (pour simplifier l'écriture, on note (u;v) l'angle
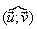 )
) - (-u; v)=(u; -v) =(u; v)+a où a est l'angle de mesure p
- d'où en termes de mesures si q est la mesure de (u;v), alors – q(2p) est la mesure de (v;u)
- et q + p(2p) est la mesure de (-u;v).
- (u;w)=(u;v)+(v;w)
- d'où en termes de mesures si q est la mesure de (u;w), a la mesure de (u;v) et b la mesure de (v;w), on a
q = a + b (2p).
- d'où en termes de mesures si q est la mesure de (u;w), a la mesure de (u;v) et b la mesure de (v;w), on a
NB: veiller à utiliser les "modulo 2 " pour les mesures d'angles mais pas pour les angles car cela n'aurait aucune signification.
1.4 Multiplication par un réel
- on a pour les mesures
 =
=
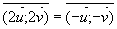 (2p)
(2p) - On a aussi
 =
=
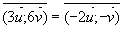 (2p)
(2p) - Mais par contre

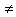
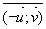 (2p)
(2p)
- Plus exactement
 =
=
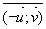 + p(2p).
+ p(2p).
- Plus exactement
On peut donc généraliser le processus :
 =(ku;lv) (2p) si k et l sont deux réels de même signe
=(ku;lv) (2p) si k et l sont deux réels de même signe =(ku;lv) + p(2p) si k et l sont deux réels de signe contraires.
=(ku;lv) + p(2p) si k et l sont deux réels de signe contraires.
Remarque :on utilise souvent des vecteurs unitaires pour définir les angles orientés;
ainsi l'angle (OA;OB) a pour mesure  si
si 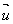 =
=
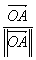 et si
et si 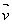 =
=
 .
Alors on a clairement
.
Alors on a clairement 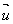 et
et
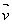 de norme 1 donc unitaires.
de norme 1 donc unitaires.
2 Bases orthonormales directes
Si 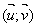 est une base orthonormale du plan orienté, cette base peut être directe ou indirecte.
est une base orthonormale du plan orienté, cette base peut être directe ou indirecte.
On dit qu' elle est directe si 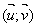 = p/2 (2p)
= p/2 (2p)
et qu'elle est indirecte si 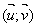 = -p/2 (2p).
= -p/2 (2p).

Ainsi pour tout vecteur unitaire du plan, il existe un vecteur
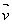 tel que
tel que
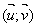 forme une base orthonormale
directe du plan. C'est pour cela qu'on parle habituellement de
(O, ,
forme une base orthonormale
directe du plan. C'est pour cela qu'on parle habituellement de
(O, ,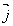 ) qui est un repère orthonormé
direct.
) qui est un repère orthonormé
direct.
3 Cosinus et sinus d'un angle orienté de deux vecteurs
Soit un angle, soit a une mesure de cet angle, c 'est à dire
que l'on a a =  .
.
DEFINITIONS:
- le cosinus de l'angle (u;v) est un nombre réel noté cos.
- Le sinus de l'angle (u;v) est un nombre réel noté sin.
- On a donc cos (u;v)=cos a et sin (u;v)=sin.
On doit connaître des valeurs dites remarquables de cosinus et sinus.
| Angle en Degrés | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 |
|---|---|---|---|---|---|---|---|---|---|
| Angle en Radians | 0 | p/6 | p/4 | p/3 | p/2 | 2p/3 | 3p/4 | 5p/6 | p |
| Cos | 1 | 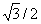 |
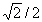 |
1/2 | 0 | -1/2 | 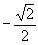 |
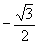 |
-1 |
| Sin | 0 | 1/2 | 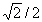 |
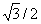 |
1 | 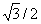 |
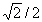 |
1/2 | 0 |
Un bon moyen pour retenir ce tableau est de se référer au cercle trigonométrique.
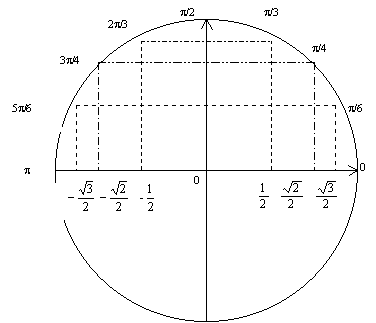
4 Coordonnées d'un vecteur dans une base orthonormale directe
Si on a un repère orthonormé direct (O, ,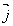 ), et A un point fixé, quelles sont les coordonnées du vecteur OA?
), et A un point fixé, quelles sont les coordonnées du vecteur OA?
On dit que a est une mesure de.
Posons 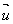 =
=
 ;
;
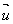 est donc un vecteur
unitaire (de norme 1) et on a aussi a =
est donc un vecteur
unitaire (de norme 1) et on a aussi a =
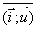 (2p).
(2p).
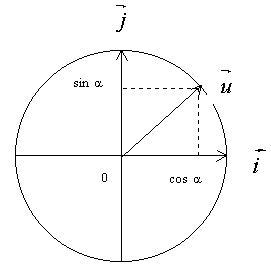
On voit clairement quelles sont les coordonnées de 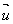 en le projetant sur l'axe des abscisses
en le projetant sur l'axe des abscisses 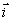 puis
en le projetant sur l' axe des ordonnées.
puis
en le projetant sur l' axe des ordonnées.
On a alors 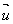 = cos
a
= cos
a 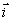 +
sin a.
+
sin a.
Et comme 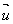 =
=
 alors
alors
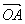 =
=
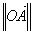 x cos
a x
x cos
a x 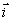 +
+
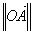 x sin a x.
x sin a x.
En bref, si 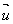
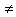
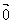 et dans
(O, ,
et dans
(O, , 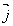 )
repère orthonormé direct, si a est une mesure de (i;u)(2p),
on a
)
repère orthonormé direct, si a est une mesure de (i;u)(2p),
on a 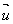 (
(
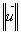 x cos
a ;
x cos
a ;
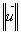 x sin a ).
x sin a ).
4.1 Avec le produit scalaire
- Si a est une mesure de l'angle orienté (u;v) alors.
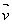 =
=
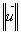 x
x
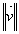 x
cos a.
x
cos a. - Si on a un repère orthonormé direct et un vecteur
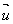 alors on a.
alors on a.
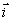 = x et.
= x et.
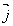 = y.
= y. - cela nous donne les coordonnées de, en l' occurrence, les coordonnées sont
x =
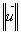 x cos a et
y =
x cos a et
y = 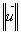 x sin a.
x sin a. - D'où on peut utiliser la formule dans l'autre sens.(c' est une utilisation importante dans les exercices à laquelle on ne pense pas toujours.)
Si on a les coordonnées de 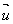 et,
et si a est une mesure de (u;v), on peut calculer cos (u;v): cos a
= (
et,
et si a est une mesure de (u;v), on peut calculer cos (u;v): cos a
= (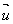 .
.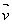 ).
Dans le cas déjà vu du vecteur
).
Dans le cas déjà vu du vecteur 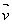 orthogonal unique formant une base orthonormée directe avec, si
orthogonal unique formant une base orthonormée directe avec, si 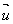 =x
=x 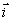 + y,
alors
+ y,
alors 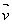 = -y
= -y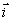 +x
+x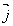 (
(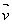 est normal car.
est normal car.
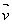 = 0 et de plus
= 0 et de plus
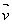 a la même norme que
a la même norme que
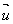 ).
).