Lois de la dynamique - travail, puissance et énergie
1 Première loi de Newton
1.1 Système pseudo-isolé
Un système est pseudo-isolé lorsqu’il est soumis à des forces extérieures qui se compensent.
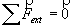
1.2 Enoncé du principe d'inertie
Il existe des référentiels dits galiléens dans lesquels un point particulier d’un solide isolé ou pseudo-isolé, appelé centre d’inertie (C.I.) :
- soit conserve son état de repos
- soit est animé d’un mouvement rectiligne uniforme, c’est-à-dire d’un mouvement dans equel le vecteur vitesse instantanée est constant.
1.3 Le C.I. est un barycentre
Soit un solide décomposé en n éléments de matière A1, A2, …,
Ai, …, An, de masse d’inertie
m1, m2, …, mi, …, mn. Le barycentre G des n éléments Ai
affectés chacun de sa masse mi défini
par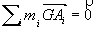 
est le centre d’inertie du solide.
2 Deuxième loi de Nexton
2.1 Notion de cinématique
Trajectoire
Pour repérer la position d’un point matériel M on utilise un repère à trois dimensions (O, i, j, k).
Celle-ci peut être définie par le vecteur position :
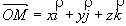
Vecteur vitesse
C’est l’expression mathématique de la dérivée du vecteur position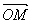 
par rapport à la variable temps.
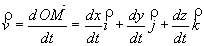
Le vecteur vitesse, à l’instant t, d’un point matériel M, est tangent en M à la trajectoire
et orienté dans le sens du mouvement. Le carré de sa valeur est donné par la relation :
v²=v²x+v²y+v²z.
Vecteur accélération
Le vecteur accélération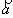 
est la dérivée par rapport au temps du vecteur vitesse.
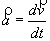
Dans le cas d’une trajectoire plane, on peut utiliser le repère de projection de Frenet associé au point mobile (M, t, n).t est le vecteur unitaire tangent à la trajectoire, orienté suivant le sens positif de la trajectoire. n est le vecteur normal unitaire orthogonal à t, et orienté vers l’intérieur de la trajectoire.
On a ainsi :
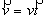et
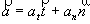avec
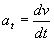et,
R étant le rayon de courbure de la trajectoire.
2.2 Etude cinématique de quelques mouvements
Mouvement rectiligne uniforme
Dans ce cas, la trajectoire est rectiligne et le vecteur vitesse
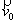est constant. D’où, l’accélération est nulle.
Si à t = 0, x = x0, l’expression de x en fonction du temps, notée x(t), est :
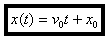
Mouvement rectiligne uniformément varié
Un point matériel est animé d’un mouvement rectiligne uniformément varié si son mouvement est rectiligne et son vecteur accélération constant.
Si à t = 0, v = v0, on en déduit :
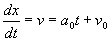
d’où :
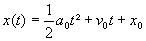
En éliminant la variable t entre les expression de v et de x, on obtient une relation
indépendante du temps très utile :
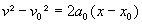
2.3 Théorème du centre d'inertie
Enoncé de la deuxième loi de Newton (relation fondamentale de la dynamique)
Dans un référentiel galiléen, la somme vectorielle
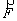des forces appliquées à un
point matériel est égale à la dérivée par rapport au temps du produit de sa masse
et de sa vitesse :
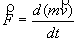
Dans l’approximation newtonnienne, la masse est constante. La deuxième loi de Newton s’écrit donc :
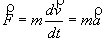
Enoncé du théorème du centre d’inertie
Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un solide est égale
au produit de sa masse et du vecteur accélération de son centre d'inertie.
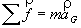ou
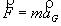
3 Cinématique, travail et énergie
3.1 Cinématique du mouvement circulaire uniforme
Repérage du point P
Pour un point matériel P animé d’un mouvement circulaire, l’abscisse curviligne s, le rayon
polaire r et l’angle polaire q sont liés par la relation :
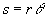
Les coordonnées polaires sont liées aux coordonnées cartésiennes par les relations :
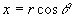et
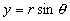
Vitesse et accélération
Le vecteur vitesse instantanée et la vitesse angulaire sont liés par la relation :
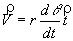
Dans le cas d’un mouvement circulaire uniforme,
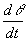est
une constante notée w. Si q = 0 à la date t = 0, l’équation horaire du mouvement circulaire uniforme est q = w t et
l’expression de
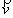devient :
Dans le mouvement circulaire uniforme de rayon r, le vecteur accélération est normal à
la trajectoire et orienté vers son centre :
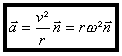
3.2 Quelques exemples
Mouvement d’un satellite
Les valeurs de la vitesse et de la période de révolution d’une planète autour du Soleil sont :
( dans l’approximation d’un mouvement circulaire )
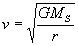
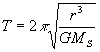
avec MS : masse du Soleil.
La vitesse et la période de révolution ne dépendent pas de la masse de la planète.
Les valeurs de la vitesse et de la période d’un satellite autour de la Terre sont :
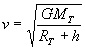
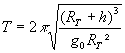
avec MT : masse de la Terre et h : altitude du satellite et RT rayon terrestre.
Mouvement d’une particule chargée dans un champ magnétique
La force de Lorentz qui s’exerce sur une particule chargée en mouvement dans un champ magnétique
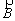a pour expression :
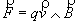
Le mouvement d’une particule chargée dans un champ magnétique est uniforme.
Le rayon de la trajectoire d’une particule chargée entrant dans un champ magnétique uniforme
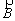avec une vitesse
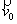orthogonale à
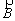a pour expression :
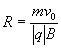
Dans un tube cathodique, la déflexion magnétique du faisceau d’électrons a pour expression :
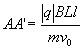
avec L : profondeur du tube et l : largeur du tube (Attention, l est la longueur de la zone ou B
existe et non la largeur du tube qui correspond à la largeur de l’écran de TV )
Dans un spectromètre de masse, le rayon de la trajectoire d’un ion, de charge q et de masse m,
accéléré sous une tension U est donné par la relation :
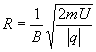
3.3 Travail et puissance d'une force
Si une force constante
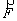voit son point d’application se déplacer de façon rectiligne de A vers B,
le travail
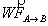de la force au cours du déplacement est par définition égal au produit scalaire du vecteur force
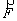par le vecteur déplacement
:
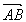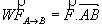ou
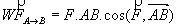
avec F en N (Newton), AB en m et W en J (Joules).
Le travail d’une force constante dans un déplacement quelconque ne dépend pas de la trajectoire du point d’application de la force, mais uniquement de ses positions initiale et finales.
Pour le calcul du travail du poids d’un solide, tout se passe comme si les forces de pesanteur étaient
équivalentes à une force localisée
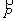appliquée au centre d’inertie G du solide.
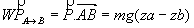
avec za-zb différence d’altitude entre les positions initiale et finale du centre d’inertie.
Le travail d’un ensemble de forces constantes agissant sur un solide en
translation est égal au produit scalaire du vecteur somme
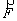des forces constantes par le vecteur, A et B étant les positions initiale et finale d’un point du solide.
Le travail de la force de frottement dépend de la trajectoire suivie par le solide entre A et B.
Le travail de la force électrostatique lors du déplacement d’une charge donnée, de A vers B,
dans un champ électrostatique uniforme, ne dépend que de la différence de potentiel entre les points
de départ et d’arrivée.
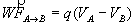
La puissance instantanée d’un ensemble de forces s’exerçant sur un solide en translation est égale
au produit scalaire du vecteur somme des forces
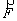par le vecteur vitesse
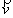du solide.
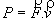
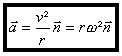
3.4 Les énergies
Energie cinétique
Entre deux instants t1 et t2, la variation D Ec de l’énergie cinétique d’un solide animé
d’un mouvement de translation par rapport à un référentiel galiléen est égale à la somme
algébrique des travaux de toutes les forces extérieures qui sont appliquées au solide entre
ces deux instants.
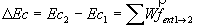
Energie potentielle
Lors du passage d’un état 1 à l’état 2, la variation d’énergie potentielle d’un système est
l’opposé du travail de la force qui caractérise l’interaction.
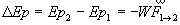
Ainsi, lorsque le solide se déplace, le travail de son poids est opposé à la variation de son énergie potentielle de pesanteur.
Energie mécanique
Dans un référentiel galiléen :
- l’énergie mécanique d’un solide soumis uniquement à des forces conservatives est une constante du mouvement
- l’énergie mécanique d’un solide soumis à un ensemble de forces, dont certaines ne sont pas conservatives, n’est pas constante et sa variation entre deux instants est égale au travail des forces non conservatives entre ces deux instants.
